Lab 7 Dipole Moment of Permanent Magnet using Compass
Permanent magnets are materials that have a magnetic moment even in the absence of an applied magnetic field. This provides the ability to "stick" to a surface, such as a refrigerator magnet. The strength of the magnet can be expressed as the magnetic dipole moment \(\mu\). The dipole moment is an approximation valid far away from the dipole. Thus, sufficiently far from the magnet, the magnetic field is \(B(r) = \frac{\mu_0}{4\pi}\frac{2\mu}{r^3}\), where r is the distance from the center of the magnetic dipole to the observation location. A so-called Hall probe could determine the magnetic field magnitude, but it is an expensive toll. Alternatively, a compass can be used to measure the magnetic field magnitude. A compass' needle far from the magnetic dipole will point in the northerly direction, but close to the magnet, the "north" arrow of the compass points towards the "south" pole of the permanent magnet. Therefore, the direction of the compass needle is affected by the constant Earth's magnetic field and the distance-varying magnetic field of the permanent magnet. Similar to the instructions in the textbook, the compass will point in the direction given by the superposition of the Earth's magnetic field and the magnetic field from the permanent magnet.
Note that the permanent magnet should have its magnetic dipole axis perpendicular to the Earth's magnetic field.
7.1 Goals
- Measure the magnetic field strength using a compass
- Determine the dipole moment of a permanent magnet
- Learn about a fitting procedure
7.2 Prediction
- Make a graph of the magnetic field versus the distance for a magnetic dipole.
- Derive an equation that relates the angle measured from the compass and the magnetic field strength, so that you have a function for \(B(r)\).
- Find the Earth's magnetic field in Long Beach at NOAA; both horizontal and vertical components of the magnetic field; Long Beach is roughly at 33.8\(^o\) N and 118.2\(^o\) W: https://www.ngdc.noaa.gov/geomag-web
7.2.1 Caution
- The permanent magnet could damage credit cards and interfere with other electro-magnetic devices.
- NdFeB magnets are very strong and you should handle them with care; i.e. avoid bringing two NdFeB magnets close to each other.
- The compass needle could get re-magnetized, if you bring a NdFeB magnet too close. Therefore, move the magnet slowly and observe the compass response carefully.
7.3 Equipment
- Compass
- Permanent Magnet
- Ruler to measure distance
7.4 Procedure
- Find the direction of the magnetic North (South) Pole and align the ruler perpendicular to that direction; i.e. ruler should point along the W-E direction.
- Vary the distance \(r\) between the compass and permanent magnet and record the compass needle’s angle. Find locations along the ruler, where you observe measurable changes in the measured angle.
- Record the angle in accordance with your diagram; note that the angle may be different from the reading on the compass.
- Compute the magnetic field at several locations, at least 10 different locations
- Determine the magnetic dipole moment of the magnet.
7.5 Measurement
Measure the angle as a function of distance, record at least 10 angles. Estimate the uncertainty of the angle, then propagate the uncertainty. Clearly define which angle \(\theta\) represents in a diagram in your notebook.
Create a table similar to this one, where \(\ln(r)\) is the natural log of the separation distance \(r\).
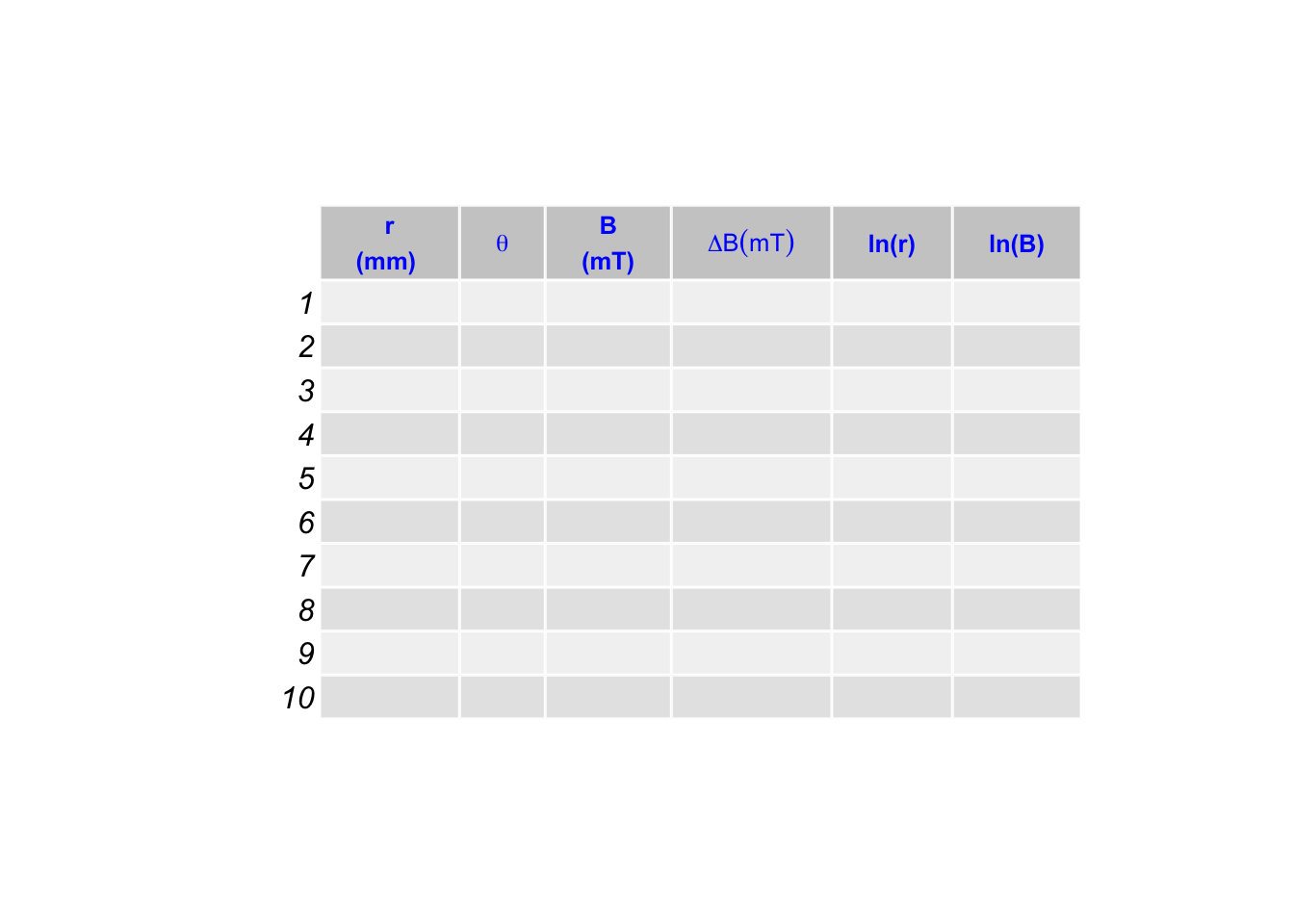
Given \(B(r) = \frac{\mu_0}{4\pi} \frac{2\mu}{r^3}\), take the natural log of this equation. It follows that \(\ln(B) = \ln \left[ (\mu_0/4 \pi)2 \mu \right] - 3 \ln(r)\) with the first part being a constant. This process is called linearization of the equation. It makes it easy for fitting. Now, graph \(\ln(B)\) versus \(\ln(r)\), you would expect to get an equation of the form y = b + mx, where m is the slope and b the offset.
Use a ruler to determine the y-intercept \(b = \ln \left[ (\mu_0/4 \pi)2 \mu \right]\) and calculate the dipole moment \(\mu\). Alternatively, use a fitting program to find the intercept. The slope \(m\) should be negative and close to 3, if the magnet is mostly a dipole.
7.6 Graph
Graph your data points for \(B(r)\) and also compute a line based on the prediction for a magnetic dipole. The measured data should be points, while the calculated data is represented as a line.
7.7 Summary
List your dipole moment \(\mu\) for the magnet, provide an uncertainty. Compare your dipole moment with the results from your class and also the value given in the M&I book. Discuss the shape of the magnetic field with distance from a dipole, mention any additional observations that you have made.