Siteswap Fractals
I used siteswap juggling patterns to generate the fractal images below. You can click on any of the images for a larger version.
If you have suggestions or feedback about these pictures, I'd love to hear them!
441

531

534

645

71

753
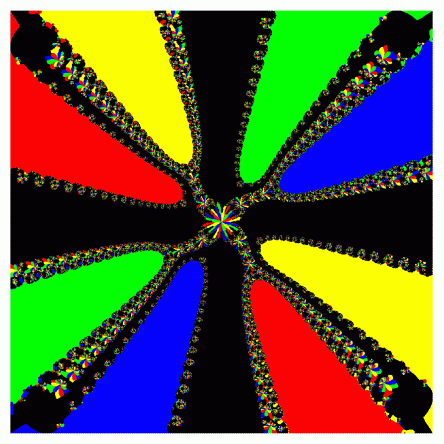
How I made these images
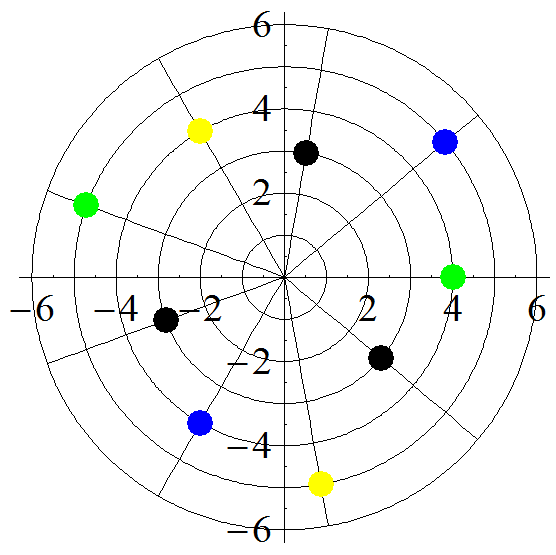
First, I arranged the balls for a particular pattern around in a circle. For example, for 534, the sequence of colors is Blue, Black, Yellow, Green, Black, Blue, Yellow, Black, Green. I moved each one out to a radius proportionate to the corresponding number, as in the picture below. (Start with the blue ball at the upper right and read around counterclockwise.)
Next, I tested every other point in the plane and computed which of the nine balls it was most "attracted" to. (That's the non-mathematical explanation; for the mathematical explanation, see the next paragraph.) If a point was attracted to a black ball, I colored it black, and so on. As you can see in the final picture for 534 above, the points that are closest to the first blue ball were all attracted to that ball, so they all got colored blue, creating a blue "sector", and so on. However, the points near the boundaries between sectors have trouble deciding which ball to be attracted to, and they often end up attracted to a completely different ball far away. That's why you get the crazy fractal designs at the boundaries.
If you know a little calculus, here's what I mean by points being "attracted" to one of the balls. First, think of the plane above as the set of complex numbers, and each point is a complex number. The nine balls represent nine complex numbers, and I made a polynomial whose roots are those nine numbers. Then for each other point in the plane, I ran Newton's Method and determined which of the nine roots the algorithm converged to.
Here's one more picture of 71, only this time turned inside out via a reflection through a circle of radius 10:
71 Inverted

Will's home page

