BASIC TESTS FOR MODELS OF THE LIP REED
R. Dean Ayers
Department of Physics and Astronomy
California
State University, Long Beach
Long
Beach, CA 90840-3901
Abstract
Simple lip reed models treat the brass player�s
upper lip as a single mass that moves with one or two degrees of freedom.
Helmholtz�s outward-swinging door model operates at a playing frequency that is higher than both the lip frequency and the relevant air
column resonance frequency. A
simple empirical test with an isolated mouthpiece shows a very different
behavior and favors either the sliding door or a two-dimensional hybrid model.
One can easily play the mouthpiece well below its resonance or
�popping� frequency, but not above it.
A similar behavior is observed in �bending� notes on the first few
usable resonances of the complete instrument.
An operational definition for the lip frequency includes both the
mechanical influence of the mouthpiece rim and acoustic feedback from the cup
and throat, which act as a Helmholtz resonator.
When the mouthpiece is attached to the complete instrument, an open
shunt hole in the backbore provides an ad
hoc approximation to that frequency.
The playing frequency is measured just after closure, before the
embouchure can be modified. A
plot of playing frequency versus lip frequency shows good agreement with the
hybrid model�s behavior at low frequencies.
No simple model gives the correct behavior for higher playing
frequencies, which drift above the resonance frequency but remain below the
lip frequency.
Stroboscopic
observations reveal a wave disturbance in the mucosa of the upper lip, much
like that on the surface of water but turned upside down.
Within the narrow passageway between the lips, the air stream drives
the mucosal wave, which in turn acts as a valve for the volume velocity
injected into the mouthpiece. More realistic models should result from using several masses
and taking advantage of existing results for the similar behavior of the vocal
folds.
INTRODUCTION
The question of how the lip reed driver for a brass
instrument actually operates is a long-standing problem that has yet to
receive a definitive answer. What
is the correct description of its motion?
How does that motion modulate the volume velocity injected into the
mouthpiece, and how is it influenced by acoustic feedback from the
instrument�s air column? An
extensive list of references on this topic is included in a recent article by
Cullen, Gilbert and Campbell [1].
Currently
three simple lip reed models are under consideration. According to Helmholtz�s outward-swinging door model, the
lips are blown open by a positive pressure difference between the mouth and
the cup of the mouthpiece. A
sliding door model has the lips being pulled together by a drop in pressure in
the air stream passing between them (Bernoulli�s principle).
Computer simulations in the time domain carried out by Adachi and Sato
have confirmed earlier theoretical results for these models [2].
Those authors have also introduced a two-dimensional hybrid model that
incorporates both driving forces by allowing orbital motion [3].
Attempts
to relate experimental results to these models, especially the two older ones,
tend to be quite confusing. The
lips are interpreted as acting sometimes like one model and sometimes like
another, and often we are left with new mysteries rather than answers.
This paper presents some very simple experiments, which are actually
little more than careful observations, as a contribution toward clearing up
that confusion.
SIMPLE EMPIRICAL TESTS
The outward-swinging door behaves differently
from the other simple models in that its playing frequency is higher than that
of the relevant peak in the air column�s input impedance.
The ability of a brass player to �bend� or drop the playing
frequency smoothly and continuously to well below the second or third
resonance frequency of the instrument provides clear evidence that this is not
a valid model for the real lip reed. Attempts to push a note sharp from an input impedance peak
have little effect, and trying too hard causes it to jump up to the next peak.
Chen
and Weinreich investigated the behavior of the lip reed while it was driving a
Helmholtz resonator [4]. With
only one impedance peak, there could be no regime of oscillation.
A simplified version of that experiment can be performed by playing on
an isolated mouthpiece. Figure 1 shows waterfall plots of acoustic spectra in the
mouthpiece as the lips are buzzed into (a) a trombone mouthpiece, (b) a
trombone mouthpiece adapted to use a trumpet rim, and (c) a trumpet
mouthpiece. Time increases from
front to back, with each plot showing a continuous glide upward, then one that
drops in pitch, and finally the lowest frequencies for that rim size.
The broken curve superimposed on each plot shows the spectrum of the
brief �pop� from slapping the rim against the palm of one�s hand.
The
inside diameter of the mouthpiece rim has a significant influence on the
behavior of the lip reed. The
small rim size of a trumpet or French horn mouthpiece makes it easier to buzz
the lips at higher frequencies and imposes a vague low frequency limit, with
or without the rest of the mouthpiece. The
large rim diameter suitable for a trombone facilitates reaching lower
frequencies, as can be seen by comparing the top portions of plots (a) and (b)
in Fig. 1. However it also
requires more �muscling� of the embouchure to play higher frequencies,
comparable to the condition of buzzing into open air without the aid of a rim.
The
most striking feature in these three plots is the sharp cutoff in response of
the lips very close to the input impedance peak.
Some hysteresis effects are visible here, with the upward glide ending
slightly higher than the frequency at which the lips start to respond in the
downward glide. The spectrum
analyzer used to generate these plots is convenient but hardly necessary for
conducting this simple test; Helmholtz could have done it by ear.
The brief �pop� produced by a hand slap on the rim lasts long
enough to hear the pitch of the impedance peak, particularly for the larger
mouthpieces.
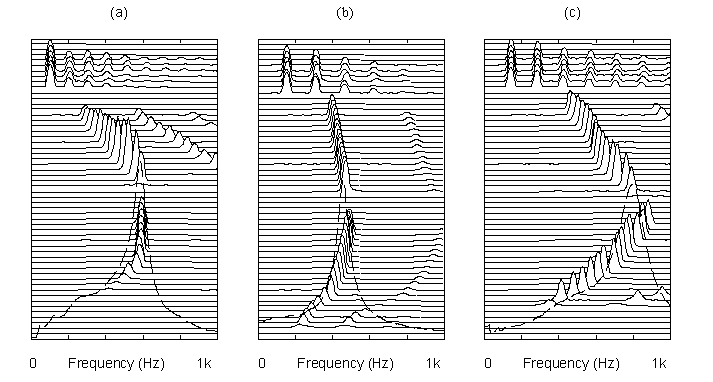
Figure
1.
Waterfall spectra (time increasing front to back): upward glide,
downward glide, then lowest pitches for rim size.
Broken curve: spectrum from �popping� the mouthpiece rim by hand.
EXPERIMENT WITH
A SHUNTED MOUTHPIECE
The simple tests of the previous section rule
out the outward-swinging door model, but they do not distinguish between the
sliding-door and hybrid models, both of which operate below the relevant
resonance frequency. In order to
compare those models with real lips we must have a means of measuring a �lip
frequency.� Unlike the mass and
spring combinations of the simple models, a real upper lip cannot be plucked
and allowed to perform damped oscillations.
(The implausibility of a lip moving as a lumped element at even a few
hundred hertz provides a good clue about its real motion.)
The
influences of the mouthpiece rim and acoustic feedback from the cup and throat
are always present, and they are essentially immediate compared to that of the
delayed reflections in the air column of the complete instrument.
This suggests that an operational definition for the lip frequency
should include those unchanging influences but not the resonance effects
arising in the rest of the air column. A
simple ad hoc approximation to that
condition is achieved by opening a shunt hole (6.35 mm diameter, in a short
chimney) in the backbore of the mouthpiece.
Figure 2 shows the input impedance curves for a complete trumpet with
the shunt hole closed (solid) and with it open (broken).
Failure to close off the rest of the air column when the hole is open
gives rise to the notches seen in the broken curve.
These do not interfere with playing an arbitrary frequency except near
the main peak, which is shifted to the right under playing conditions by lip
intrusion into the cup.
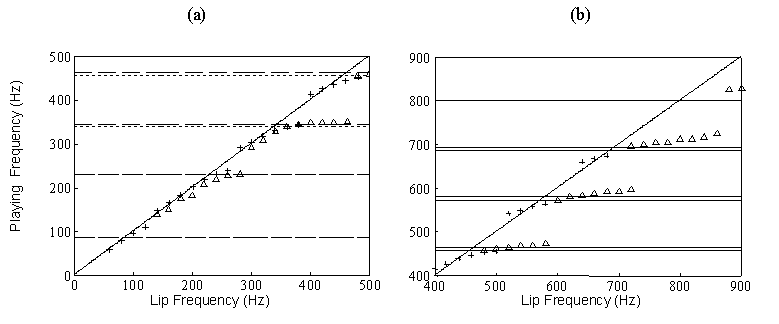
The performer first stabilizes the frequency close to a desired value with the hole open. Then the hole is closed without interrupting the sound and the playing frequency for the complete instrument is captured very quickly, so that the embouchure is still set for the open hole lip frequency. In Fig. 3 the results of this experiment are compared with computational results for the outward-swinging and sliding door models, which were obtained in time domain simulations by Adachi and Sato [2]. Horizontal lines show the resonance frequencies: dashed = experimental values; dotted = those of Adachi and Sato. There is clear disagreement between the Helmholtz model and the experimental results in the relationship of the playing frequency to both the lip frequency and the resonance frequencies. The sliding door model agrees well with the experimental results for the second resonance (the first one used on the trumpet), but above that the two behaviors differ noticeably.
The same experimental results are also shown in Fig. 4, with computational results for the two-dimensional hybrid model of Adacho and Sato [3]. Both frequency scales have been expanded and the entire plot has been broken into two parts to show the close agreement of the two behaviors, especially for the second and third resonances. The discrepancies in the lip frequencies at which the playing frequency shifts up to the neighborhood of the next resonance seem to indicate that feedback from the air column has a stronger influence on the actual lip reed than on this model, especially at higher frequencies. Small adjustments in the model's parameters may reduce that disagreement.
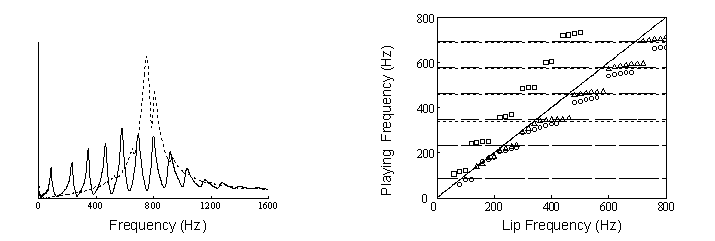
Figure 2. Trumpet input impedance curves. Figure 3. Playing frequency vs. lip frequency:
Solid: normal (shunt hole closed). * = swinging door model
Broken: shunt hole open. O = sliding door model
) = this experiment