Back to Problems

Mathematica code for Animating Taylor Series Expansion

H.Tahsiri

Clear[f,p]

f[x_]=Sin[x]

     Sin[x]

(* poly[x,n] is an approximate polynomial of f[x] obtained by
 Taylor expansion of f[x],of order n, near x0 *)

Do[poly[x_,n]=Series[f[x],{x,0,n}]//Normal,{n,1,9}]

poly[x,9]

          3    5      7       9
         x    x      x       x
     x - -- + --- - ---- + ------
         6    120   5040   362880

(* f[x] is in red amd poly[x,n] is blue*)

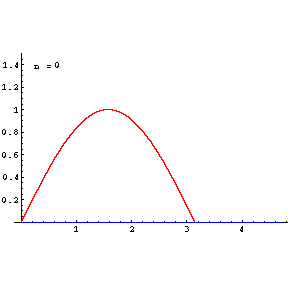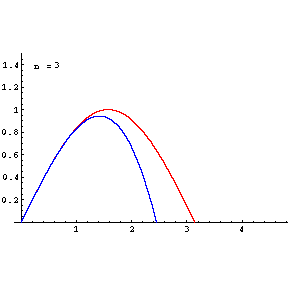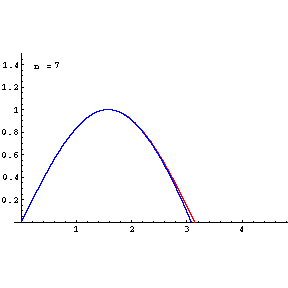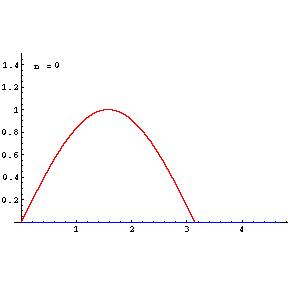
Do[Plot[{f[x],poly[x,n]},{x,0,3Pi/2},PlotRange->{0,1.5},
Epilog->{{Text["n =  ",{0.5,1.4}]},{Text[n,{.65,1.4}]}},
PlotStyle->{RGBColor[1,0,0],RGBColor[0,0,1]}],{n,0,9}]

RED=f(x)=sin(x)

BLUE=TaylorPolynomial of order n=1,2,3,4,5,6,7,8,9

Note:As shown in plot and the list below, for largr value of n=9, poly[x,n] becomes equal to f[x]

when the remainder converges to zero.

remainder[x_,n_]=f[x]-poly[x,n]

     -poly[x, n] + Sin[x]

                                               -7                      -7                     -13
     {0.00999983333416667, -1.66665833335744 10  , -1.66665833335744 10  , 8.33331667560167 10   , 
      
                          -13                       -18                       -18
       8.33331667560167 10   , -1.734723475976807 10   , -1.734723475976807 10   , 0., 0., 0.}

Back to Problems