A possitive charged rod
H.Tahsiri
A thin non-conducting rod of finite length L carries a total charge
Q,spread uniformly along it.
a) Find the components of the electric fields.
b) find y-component of the electric field for ( L-> infinity >> y ) by two different methods
i) by taking the limit. ii) by direct integration.
Enter the above equations in the Mathematica notebook
as follow.
Ey=lamda 1/(4Pi eps0) y Integrate[1/(x^2+y^2)^(3/2),{x,-L/2,L/2}]
L lamda
---------------------------
2 2
2 eps0 Pi y Sqrt[L + 4 y ]
Ex=lamda 1/(4Pi eps0) y Integrate[x/(x^2+y^2)^(3/2),{x,-L/2,L/2}]
0
EylargeL=Limit[Ey,L->Infinity]
lamda
-----------
2 eps0 Pi y
EylargeL=lamda 1/(4Pi eps0) y Integrate[1/(x^2+y^2)^(3/2),
{x,-Infinity,Infinity}]
lamda
-----------
2 eps0 Pi y
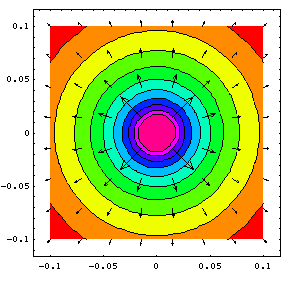
Plot the electric field lines in the z-y plane.
This problem has cylindrical symmetry with respect to the x-axis
at all points in the yz plane
of radius y=r from the charged rod.
Enter the z and the y components of the electric field as follow.
Ezcompnt=lamda L z/(2 Pi eps0 (z^2+y^2) Sqrt[L^2+4(z^2+y^2)])
L lamda z
------------------------------------------
2 2 2 2 2
2 eps0 Pi (y + z ) Sqrt[L + 4 (y + z )]
Eycompnt=lamda L y/(2 Pi eps0 (z^2+y^2) Sqrt[L^2+4(z^2+y^2)])
L lamda y
------------------------------------------
2 2 2 2 2
2 eps0 Pi (y + z ) Sqrt[L + 4 (y + z )]
given={eps0->1/(4N[Pi] 9 10^9),L=1;Q=10^(-6);lamda->Q/L};
Efield={Ezcompnt,Eycompnt}/.given//N
18000. z 18000. y
{---------------------------------, ---------------------------------}
2 2 2 2 2 2 2 2
(y + z ) Sqrt[1. + 4. (y + z )] (y + z ) Sqrt[1. + 4. (y + z )]
<<Graphics`PlotField` (* This command will load the plotting
routin for the vector field *)
Efieldplot=PlotVectorField[Efield,{z,-.1,.1},{y,-.1,.1},
PlotPoints->8,ColorFunction->None];
Clear[given,L]
V=lamda/(4Pi eps0) Integrate[1/(x^2+y^2)^(1/2),{x,-L/2,L/2}]
2 2
-L L 2 L L 2
lamda (-Log[-- + Sqrt[-- + y ]] + Log[- + Sqrt[-- + y ]])
2 4 2 4
---------------------------------------------------------
4 eps0 Pi
potential=V/.y^2->z^2+y^2
2 2
-L L 2 2 L L 2 2
lamda (-Log[-- + Sqrt[-- + y + z ]] + Log[- + Sqrt[-- + y + z ]])
2 4 2 4
-------------------------------------------------------------------
4 eps0 Pi
given={eps0->1/(4Pi 9 10^9),L=1;Q=10^(-6);lamda->Q/L};
pplot=ContourPlot[potential/.(given//N),{z,-.1,.1},{y,-.1,.1},
PlotPoints->26,ColorFunction->Hue]
ez=-D[potential,z]//Simplify//Together
lamda z
-----------------------------------------
2 2 2 2
2 eps0 Pi (y + z ) Sqrt[1 + 4 y + 4 z ]
ey=-D[potential,y]//Simplify//Together
lamda y
-----------------------------------------
2 2 2 2
2 eps0 Pi (y + z ) Sqrt[1 + 4 y + 4 z ]
together=Show[{pplot,Efieldplot}];
