Back to Problems
H.Tahsiri
UP AND DOWN MOTION OF A BALL IN VACCUM AND AIR
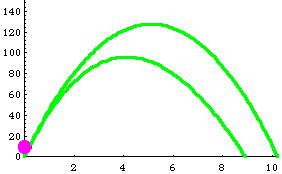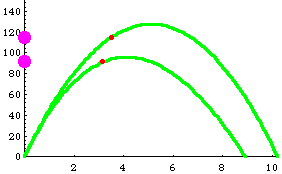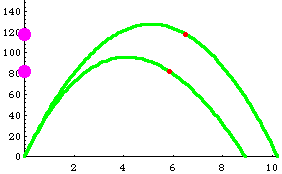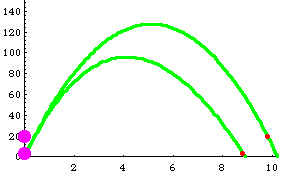
Please follow the program below to see how the above animation
is done
UP AND DOWN MOTION OF A BALL IN VACCUM
Clear[y,t,given,v0,g,y0]
given1={v0->50,g->9.8,y0->0}
{v0 -> 50, g -> 9.8, y0 -> 0}
y=y0+v0 t-.5 g t^2
2
-0.5 g t + t v0 + y0
ynoair = y/.given1
2
50 t - 4.9 t
totaltnoair=Solve[ynoair==0,t]
{{t -> 0.}, {t -> 10.2041}}
yupdownoairplot=Plot[ynoair,{t,0,10.2041}];
![[Graphics:airfrictiongr2.gif]](airfrictiongr2.gif)
![[Graphics:airfrictiongr1.gif]](airfrictiongr1.gif)
UPWARD MOTION OF A BALL IN AIR
Clear[y,v]
given2={b->.1,g->9.8,v0->50}
{b -> 0.1, g -> 9.8, v0 -> 50}
aupair=-g -b v[t]
-g - b v[t]
vupair=DSolve[{v'[t]==aupair,v[0]==v0},v[t],t]
b t
g - E g + b v0
{{v[t] -> -----------------}}
b t
b E
vupairsymbl=vupair[[1,1,2]]
b t
g - E g + b v0
-----------------
b t
b E
vupairnum=vupairsymbl/.given2
0.1 t
10. (14.8 - 9.8 E )
-----------------------
0.1 t
E
tupair=Solve[vupairnum==0,t]
{{t -> 4.12245}}
tupairvalue=tupair[[1,1,2]]
4.12245
yupair=DSolve[{y'[t]==vupairsymbl,y[0]==0},y[t],t]
b t b t b t
-g + E g - b E g t - b v0 + b E v0
{{y[t] -> -------------------------------------------}}
2 b t
b E
yupairsymbl=yupair[[1,1,2]]
b t b t b t
-g + E g - b E g t - b v0 + b E v0
-------------------------------------------
2 b t
b E
tocheck=Limit[yupairsymbl,b->0]
2
-(g t )
------- + t v0
2
yupairnum=yupairsymbl/.given2
0.1 t 0.1 t
100. (-14.8 + 14.8 E - 0.98 E t)
------------------------------------------
0.1 t
E
yupvalue=yupairnum/.t->tupairvalue
96.0001
yupairtable=Table[{t,yupairnum},{t,0,tupairvalue,.09}];
yupairplot=ListPlot[yupairtable,PlotJoined->True];
![[Graphics:airfrictiongr2.gif]](airfrictiongr2.gif)
![[Graphics:airfrictiongr3.gif]](airfrictiongr3.gif)
DOWNWARD MOTION OF A BALL IN AIR
Clear[v,t,y]
given3={b->.1,g->9.8,v0->50}
{b -> 0.1, g -> 9.8, v0 -> 50}
adownair=g-b v[t]
g - b v[t]
vdownair=DSolve[{v'[t]==adownair,v[0]==0},v[t],t]
g g
{{v[t] -> - - ------}}
b b t
b E
vdownairsymbl=vdownair[[1,1,2]]
g g
- - ------
b b t
b E
vdownairnum=vdownairsymbl/.given3
98.
98. - ------
0.1 t
E
ydownair=DSolve[{y'[t]==vdownairsymbl,y[0]==0},y[t],t]
g g g t
{{y[t] -> -(--) + ------- + ---}}
2 2 b t b
b b E
ydownairsymbl=ydownair[[1,1,2]]
g g g t
-(--) + ------- + ---
2 2 b t b
b b E
ydownairnum=ydownairsymbl/.given3
980.
-980. + ------ + 98. t
0.1 t
E
tdownair=FindRoot[ydownairnum==96.0001,{t,4}]
{t -> 4.77834}
tdownairvalue=tdownair[[1,2]]
4.77834
tupairvalue
4.12245
ydownairtable=Table[{t+tupairvalue,96.0001-ydownairnum},
{t,0,tdownairvalue,.09}];
ydownairplot=ListPlot[ydownairtable,PlotJoined->True,
AxesOrigin->{tupairvalue,0}];
![[Graphics:airfrictiongr2.gif]](airfrictiongr2.gif)
![[Graphics:airfrictiongr4.gif]](airfrictiongr4.gif)
UP AND DOWN MOTION TOGETHER
yupdownairtable=Join[yupairtable,ydownairtable];
yupdownairplot=ListPlot[yupdownairtable,PlotJoined->True];
![[Graphics:airfrictiongr2.gif]](airfrictiongr2.gif)
![[Graphics:airfrictiongr5.gif]](airfrictiongr5.gif)
together=Show[{yupdownairplot,yupdownoairplot}];
![[Graphics:airfrictiongr2.gif]](airfrictiongr2.gif)
![[Graphics:airfrictiongr6.gif]](airfrictiongr6.gif)
SIMULATION OF AN UP AND DOWN MOTION OF A BALL IN VACCUM AND
AIR
ynoair
2
50 t - 4.9 t
g=Table[{0,ynoair},{t,0,10.2,.1}];
Length[g]
103
gg=Table[{t,ynoair},{t,0,10.2,.1}];
gair=Table[{0,yupdownairtable[[i,2]]},{i,1,100}];
ggair=Table[yupdownairtable[[i]],{i,1,100}];
Length[gair]
100
Length[ggair]
100
Do[
Show[(*(Graphics[Dashing[{.008}],Thickness[.003],Line[{g[[n]],gg[[n]]}]])*)
ListPlot[gg,PlotJoined->True,PlotRange->{{0,10.20},{0,150}},
PlotStyle->{Thickness[.01],RGBColor[0,1,0]},DisplayFunction->Identity],
ListPlot[{gg[[3n]]},PlotRange->{{0,10.20},{0,150}},
PlotStyle->{RGBColor[1,0,0],PointSize[.02]},
DisplayFunction->Identity],
ListPlot[{g[[3n]]},PlotRange->{{0,10.20},{0,150}},
PlotStyle->{RGBColor[1,0,1],PointSize[.05]},
DisplayFunction->Identity],
ListPlot[ggair,PlotJoined->True,PlotRange->{{0,10.20},{0,150}},
PlotStyle->{Thickness[.01],RGBColor[0,1,0]},DisplayFunction->Identity],
ListPlot[{ggair[[3n]]},PlotRange->{{0,10.20},{0,150}},
PlotStyle->{RGBColor[1,0,0],PointSize[.02]},
DisplayFunction->Identity],
ListPlot[{gair[[3n]]},PlotRange->{{0,10.20},{0,150}},
PlotStyle->{RGBColor[1,0,1],PointSize[.05]},
DisplayFunction->Identity],
DisplayFunction->$DisplayFunction], (* end Show *)
{n,1,33}] (* end Do *)
Back to Problems


![[Graphics:airfrictiongr1.gif]](airfrictiongr1.gif)
![[Graphics:airfrictiongr3.gif]](airfrictiongr3.gif)
![[Graphics:airfrictiongr4.gif]](airfrictiongr4.gif)
![[Graphics:airfrictiongr5.gif]](airfrictiongr5.gif)
![[Graphics:airfrictiongr6.gif]](airfrictiongr6.gif)