Plank-Wien-Stefan Laws

H.Tahsiri

plankrad[lambda_,T_]=2 h c^2/((lambda^5 ( Exp[h c/(lambda k T)]-1)))

                      2
                   2 c  h
     ----------------------------------
            (c h)/(k lambda T)        5
     (-1 + E                  ) lambda

Integrate to find the total radiation output by the source with teperature T.

outputrad=Integrate[plankrad[lambda,T],{lambda,0,Infinity}][[2]]

        4   4  4
     2 k  Pi  T
     -----------
          2  3
      15 c  h

The above result shows that the total output radiation from a blackbody is proportional to the forth power of the temperature.Stefan-Boltzmann Law.

Now evaluate the amount of radiation within the visible part of the spectrum.Take this spectral region to be between 400 and 700 nanometer.

given={k->1.380658 10^(-23),h->6.626076 10^(-34),c->3 10^8.}

                     -23                 -34            8
     {k -> 1.38066 10   , h -> 6.62608 10   , c -> 3. 10 }

p6000=Plot[plankrad[lambda,6000]/.given,
{lambda,0, 1500 10^(-9)},PlotRange->{{0,1500 10^(-9)},{0,3.5 10^13}}, 
PlotStyle->RGBColor[0,0,1],Ticks->{{0,400. 10^(-9),800. 10^(-9),1200. 10^(-9)},
{0,5. 10^12,1.5 10^13,2.5 10^13,3.5 10^13}},
AxesLabel->{"wavelength","Intensity"},
Epilog->{{Text["T = 6000 K ",{1.3 10^(-6),1.5 10^13}]}}];

p5000=Plot[plankrad[lambda,5000]/.given,
{lambda,0, 1500 10^(-9)},PlotRange->{{0,1500 10^(-9)},{0,3.5 10^13}}, 
PlotStyle->RGBColor[1,0,0],Ticks->{{0,400. 10^(-9),800. 10^(-9),1200. 10^(-9)},
{0,5. 10^12,1.5 10^13,2.5 10^13,3.5 10^13}},
AxesLabel->{"wavelength","Intensity"},
Epilog->{{Text["T = 5000 K ",{1.2 10^(-6),1 10^13}]}}];

p4000=Plot[plankrad[lambda,4000]/.given,{lambda,0, 1500 10^(-9)},
PlotRange->{{0,1500 10^(-9)},{0,3.5 10^13}}
PlotStyle->RGBColor[1,0,1],
Ticks->{{0,400. 10^(-9),800. 10^(-9),1200. 10^(-9)},
{0,5. 10^12,1.5 10^13,2.5 10^13,3.5 10^13}},
AxesLabel->{"wavelength","Intensity"},
Epilog->{{Text["T = 4000 K ",{8  10^(-7),1  10^13}]}}];

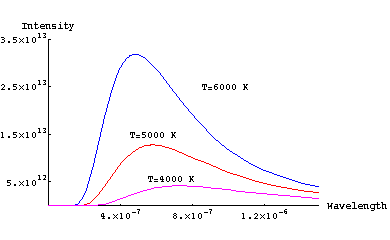
planktogether=Show[{p6000,p5000,p4000},

Epilog->{Text["T=6000 K ",{1 10^(-6),2.5 10^13}],Text["T=5000 K ",{6 10^(-7),1.5

10^13}], Text["T=4000 K ",{7 10^(-7),5.8 10^12}]},AxesLabel->{"Wavelength","Intensity"}];

p=Do[Plot[plankrad[lambda,T]/.given,{lambda,0, 1500 10^(-9)},

PlotRange->{{0,1500 10^(-9)},{0,50 10^13}},
Ticks->{{0,400. 10^(-9),800. 10^(-9),1200. 10^(-9)},
{0,1. 10^14,2. 10^14,3. 10^14,4. 10^14,5. 10^14}},
AxesLabel->{"wavelength","Intensity"}],{T,4000,10000,1000}];

Stefan's Law

Total radiation output over all wavelenght ,when summed ove solid angles gives the Stefan law

stefan=Pi outputrad/.given

               -8  4
     5.66266 10   T

Wien's law

Plank' law, when the exponetial becomes very large compared to unity becomes

wien [lambda_,T_]=2 h c^2/((lambda^5 ( Exp[h c/(lambda k T)])))

                  2
               2 c  h
     ---------------------------
      (c h)/(k lambda T)       5
     E                   lambda

maximize=D[wien [lambda,T],lambda]//Simplify

          2
       2 c  h (c h - 5 k lambda T)
     -------------------------------
      (c h)/(k lambda T)         7
     E                   k lambda  T

maxlambda=Solve[maximize==0,lambda]/.given

                 0.00287953
     {{lambda -> ----------}}
                     T

wienplot1=Plot[wien[lambda,6000]/.given,
{lambda,0, 1500 10^(-9)},
PlotRange->{{0,1500 10^(-9)},{0,3.5 10^13}},
Ticks->{{0,400. 10^(-9),800. 10^(-9),1200. 10^(-9)},
{0,5. 10^12,1.5 10^13,2.5 10^13,3.5 10^13}}, 
PlotStyle->RGBColor[0,0,0],DisplayFunction->Identity];

wienplot2=Plot[wien[lambda,5000]/.given,
{lambda,0, 1500 10^(-9)},PlotRange->{{0,1500 10^(-9)},{0,3.5 10^13}},
Ticks->{{0,400. 10^(-9),800. 10^(-9),1200. 10^(-9)},
{0,5. 10^12,1.5 10^13,2.5 10^13,3.5 10^13}}, 
PlotStyle->RGBColor[0,0,0],DisplayFunction->Identity];